ALG 2

Here is an open version of our ALG 2 root task - a slightly more structured version will appear on Monday, with other variants later in the week.

The task starts with the idea that an unknown can vary, rather than the more common idea in school mathematics that it has a specific value that we want to find.
Also, rather than immediately asking students to perform various actions on the unknown (such as collecting like terms, manipulating or evaluating expressions, forming and solving equations), the task may help students realise that they can sometimes make sense of expressions from the outset - especially in this case, where the given expressions (x and 2x) are fairly simple, and thus might fairly readily lead to an interpretation like 'one angle in the triangle is twice the size of another angle'.
A movie of the triangle can be found here.
-
MONDAY: Here is this week's root task. It is more structured than the version above but it should still help students discern the general relationship between two of the triangle's angles (ie between the expressions x and 2x). Part b) provides a shift towards the use of algebraic procedures, by asking students to find a particular (critical) value of x. We can solve this algebraically by forming the equation x + 2x = 180. However, it is important to acknowledge that we can also find x quite easily by other means, eg trial and improvement.

 We have made two movies showing the triangle as x varies. In one movie the value of x goes up to the 'permissible' value. In the other movie the value of x goes beyond this value: what happens to the triangle when this occurs, and should such values be 'allowed'?!
-
TUESDAY: Like Monday's part b), we don't need formal algebra to solve this variant of ALG 2, but it gives us the opportunity to construct two more equations in x, so it becomes interesting to compare them and to discuss ways in which they can be solved.

 It is also worth engaging with the geometry of the situation. For example, why is the triangle always weighted to the right in the given diagrams? Also, we can see from the given triangles that the value of x will be close to 35 for one of the isosceles triangles, and somewhat less than 50 for the other - do our algebraic approaches confirm this?
-
WEDNESDAY: Having looked for isosceles triangles, this variant involves finding values of x for which the triangle is right-angled:

We can find x by using trial and improvement, say, but we can also proceed algebraically by forming equations to represent the geometric relations resulting from angle B or angle C being a right angle. This gives 2x = 90 and x + 2x = 90 (or x + 2x + 90 = 180). Similarly, we can form equations for the earlier variants: x + 2x = 180 (ALG 2A), x + 2x + 2x = 180 and x + x + 2x = 180 (ALG 2B). These equations are all fairly easy to solve, but what is particularly nice about the more complex ones is that we may be able to persuade students of their utility: by forming and writing down equations we can ease the strain on our working memory.
It can also be useful to discuss and compare different ways of solving the equations, eg by inspection, by trial and improvement, or by transforming the equations.
-
THURSDAY: Here we change the relationship between the base angles of the triangle from x˚, 2x˚ to x˚, 4x˚. This gives students a chance to recap on earlier ideas and methods, as well as perhaps starting to think about how changes in the angle relationship might affect the size of the various angles that we are trying to find.

Thursday enjoyed a couple of bonus tasks (below). The first can be varied in quite nice ways. The other [based on a seminal idea from David Fielker, writing some years ago in Mathematics Teaching] says something about the freedom that symbolic algebra can give us.

And here's another bonus (actually posted on Friday) which continues the regular polygon theme:

-
FRIDAY: This is our final (for now?) ALG 2 variant. It gives plenty of scope for consolidation and for exploring the relationship between the base angles, which is expressed here in a more general way (with the aid of parameters a and b). Let us know what you or your students find.

-

SUNDAY Supplement: Here's a set of three tasks still involving the base angles of a triangle but where there's an inverse proportional relationship. Some of the resulting triangle-families can be quite surprising.

Here's the first task (below). Part a) is to get students to start thinking about the scenario. The given information means that a/20 = 50, so a = 1000. It might seem surprising that a relation involving '1000' works in the context of triangles, where the interior angle sum is a mere 180˚. Of course, the relation ∠A = x˚, ∠B = 1000˚/x doesn't work for all values of x. For example, if x = 1, then ∠B would be 1000˚. However it turns out the relation works for this range of values (approximately): 

6 ≤ x ≤ 174.

It is worth spending quite a lot of time on part b)i, to get a feel for how the base angles, and the overall shape of the triangle, change. The triangle turns out to be fairly 'flat'. When x is 'small', a change in x produces a rapid change in ∠B; when x is fairly 'large' ∠B seems to change hardly at all. A movie of the changing triangle can be found here.

A good way to start part b)ii is to adopt a visual approach, eg by running the aforementioned movie and pausing it when the triangle looks to be isosceles. This happens in three places. A more precise estimate can then be found by using a numerical approach, which can be made more and more precise with the aid of a spreadsheet (with a column for x, for 1000/x and for 180 – x – 1000/x).

In the isosceles case where ∠A = ∠B, x = √1000. The value of x for the other two cases (∠A = ∠C and ∠C = ∠B) can be found algebraically by forming an equation in x and writing it in the usual quadratic form. However, it doesn't factorise....

-

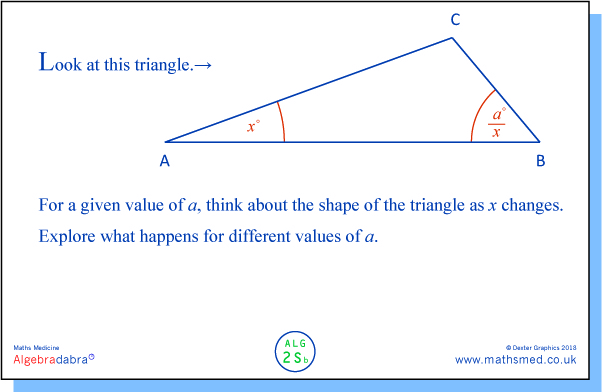
Here's the second Sunday Supplement task. This is very exploratory. You might want to start by seeing what happens with some fairly 'random' values of a, and then try some more 'informed' values.

After some explorations, you might want to look at two further movies, where a = 100 and a = 1.

The choice of '100' is very deliberate and you might like to predict what effect this has on the shape of the triangle. The effect of choosing a = 1 is very strange.... - but the movie won't win any Oscars.

-

The third Sunday Supplement:

In this task the numbers are nicer. You might be able to see the value of x for which ∠A = ∠B. The value of x for the other two isosceles cases (∠A = ∠C and ∠C = ∠B) can be found by forming a quadratic equation which this time does factorise. Or you could adopt a visual/numeric approach again, perhaps with the aide of this movie, or this second version which provides a trace of vertex C.